Principe de la méthode « diviser pour régner ».
La méthode « diviser pour régner » (‘divide and conquer’) est une méthode algorithmique basée sur le principe suivant :
- soit un problème – généralement complexe à résoudre -, ce problème est divisé en plusieurs problèmes de même nature mais de taille inférieure, l’idée étant que ces problèmes réduits en taille seront plus faciles et plus rapides à résoudre que le problème original.
- Une fois ces sous-problèmes résolus,
- leurs solutions sont combinées afin d’obtenir une solution au problème de départ.
La méthode « diviser pour régner » repose donc sur 3 étapes :
- DIVISER : division d’un problème initial complexe un certain nombre de sous-problèmes
- RÉGNER : résolution des sous-problèmes
- COMBINER : combinaison des solutions apportées aux sous-problèmes afin d’obtenir une solution au problème d’origine.
Les algorithmes basés sur la méthode « diviser pour régner » sont très souvent des algorithmes récursifs.
Il existe de nombreux exemples de problème qui peuvent être résolus par cette méthode , en particulier :
- la recherche dichotomique d’une valeur dans une liste triée (dont l’algorithme a été étudiée en Première) ;
- la méthode de tri par fusion ;
- la rotation d’une image de 90° .
Recherche dichotomique dans une liste triée
- Problème à résoudre
- Rappel : Algorithme et implémentation itérative
- Algorithme et implémentation récursive
Le problème à résoudre
Il s’agit de déterminer si un entier N apparaît dans une liste de valeurs entières, triées par ordre croissant et rangées dans un tableau T.
Algorithme : recherche dichotomique dans une liste triée
- Début de l’algorithme
Soit un tableau T de t nombres entiers, triés par ordre croissant
soit un entier n
soit d l’index de la valeur de T à partir de laquelle on effectue la recherche. Initialement d prend la valeur du plus petit index de T.
soit f l’index de la valeur de T jusqu’à laquelle on effectue la recherche. Initialement f prend la valeur du plus grand index de T.
soit m l’index de la valeur de T telle que m prend la valeur du quotient de la division entière par 2 de la somme de d et f.
soit trouve qui prend la valeur « Faux »
Tant que d est strictement inférieur à f, faire :
si n est strictement supérieur à la valeur de T située à l’index m, faire :- d prend la valeur de m plus 1
- m prend la valeur du quotient de la division entière par 2 de la somme de d et f.
- fin si
sinon si n est strictement inférieur à la valeur de T située à l’index m, faire :- f prend la valeur de m moins 1
- m prend la valeur du quotient de la division entière par 2 de la somme de d et f.
- fin sinon si
sinon faire :- trouve prend la valeur « Vrai »
- d prend la valeur f plus 1
- fin sinon
Fin tant que
Afficher trouve
- Fin de l’algorithme
Exercice 1 – Programmer en langage Python une fonction correspondant à cet algorithme.
Corrigé (solution possible)
Nom du fichier : recherche_dichotomique_iter.py
Type du fichier : text/x-python
Taille du fichier : 1 Ko
Algorithme : recherche dichotomique dans une liste triée
- Début de l’algorithme
- Soit un tableau T de t nombres entiers, triés par ordre croissant
- Soit un entier n
- soit d l’index de la valeur de T à partir de laquelle on effectue la recherche. Initialement d prend la valeur du plus petit index de T.
- soit f l’index de la valeur de T jusqu’à laquelle on effectue la recherche. Initialement f prend la valeur du plus grand index de T.
- soit m l’index de la valeur de T telle que m prend la valeur du quotient de la division entière par 2 de la somme de d et f.
- si d est strictement supérieur à f, afficher « Faux » et Fin de l’algorithme
- m prend la valeur du quotient de la division entière par 2 de la somme de d et f.
- si n est strictement supérieur à la valeur de T située à l’index m, alors faire :
- d prend la valeur de m plus 1
- exécuter algorithme de recherche dichotomique dans une liste triée
- si n est strictement inférieur à la valeur de T située à l’index m, alors faire :
- f prend la valeur de m moins 1
- exécuter algorithme de recherche dichotomique dans une liste triée
- Afficher « Vrai »
- Fin de l’algorithme
Exercice – Programmer en langage Python un fonction récursive correspondant à cet algorithme
Corrigé (solution possible)
Nom du fichier : recherche_dichotomique.py
Type du fichier : text/x-python
Taille du fichier : 2 Ko
Exercice – Déterminer le coût de cet algorithme dans le pire des cas.
Soit le tableau contenant 2 valeurs : 1 et 2 situées aux index 0 et 1. Alors m vaut (0 + 1) // 2 = 0.
La valeur située à l’index 0 est 1.
Le pire des cas est de chercher une valeur qui n’existe pas dans le tableau.
Ici 0 ou 3 par exemple.
Pour la valeur recherchée 0, celle-ci étant inférieure à 1, la recherche devrait se poursuivre entre l’index 0 et l’index 0 – 1 = -1.
L’index de fin étant inférieur à l’index de début la recherche s’arrête.
Il y a eu dans ce cas 1 division du tableau de départ.
Pour la valeur recherchée 3, celle-ci étant supérieure à 1, la recherche devrait se poursuivre dans le tableau entre l’index 1 + 1 = 2 et l’index 1.
L’index de début étant supérieur à l’index de fin la recherche s’arrête.
Il y a eu dans ce cas 1 division du tableau de départ.
Donc le coût sera de 1 division dans le pire des cas.
Soit le tableau contenant 3 valeurs : 1, 2 et 3 situées aux index 0, 1 et 2.
Alors m vaut (0 + 2) // 2 = 1.
La valeur située à l’index 1 est 2.
Le pire des cas est de chercher une valeur qui n’existe pas dans le tableau.
Ici 0 ou 4 par exemple.
Pour la valeur recherchée 0, celle-ci étant inférieure à 2, la recherche va se poursuivre dans le tableau entre l’index 0 et l’index 1 – 1 = 0. Alors m vaut 0 // 2 = 0.
La valeur à l’index 0 étant 1 donc plus grande que 0, la recherche devrait se poursuivre entre l’index 0 et l’index 0 – 1 = -1.
L’index de fin étant inférieur à l’index de début la recherche s’arrête.
Il y a eu dans ce cas 1 seule division du tableau de départ.
Pour la valeur recherchée 4, celle-ci étant supérieure à 2, la recherche va se poursuivre dans le tableau entre l’index 1 + 1 = 2 et l’index 2. Alors m = (2 + 2) // 2 = 2.
La valeur à l’index 2 étant 2, la recherche devrait se poursuivre entre l’index 2 + 1 = 3 et l’index 2.
L’index de début étant supérieur à l’index de fin la recherche s’arrête. Il y a eu dans ce cas 1 seule division du tableau de départ.
Donc le coût sera de 1 dans le pire des cas.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Tri « fusion »
- (Rappel) Algorithme de tri par insertion et par sélection
- Algorithme de tri par fusion
- Implémentation du tri par fusion en langage Python (version 1)
- Implémentation du tri par fusion en langage Python (version 2)
- Terminaison de l’algorithme
- Correction de l’algorithme
- Coût de l’algorithme
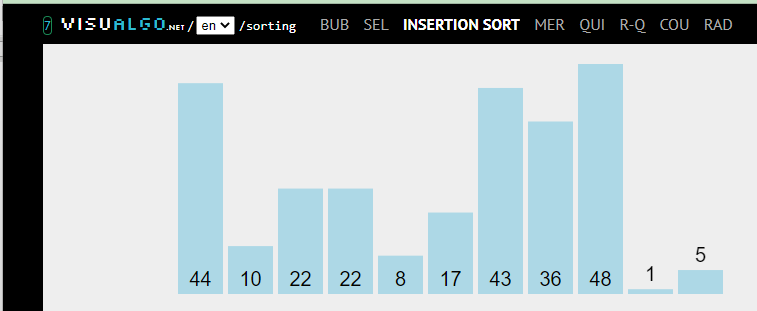
Exercice (à faire à la maison)
En vous appuyant sur le déroulement d’un tri par insertion présenté dans le vidéogramme ou dans l’animation en ligne ci-dessus :
>> écrire l’algorithme de ce tri ;
>> programmer en langage Python une fonction qui implémente cet algorithme.
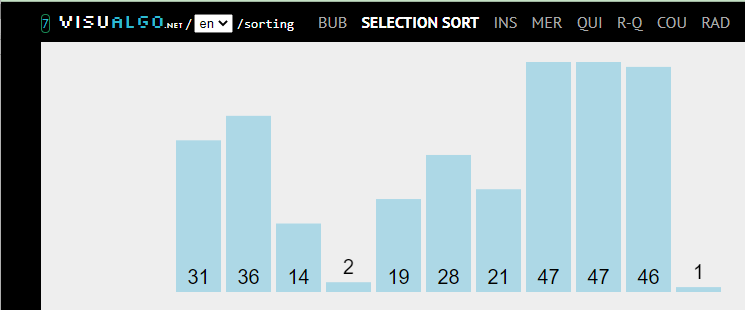
Exercice (à faire à la maison)
En vous appuyant sur le déroulement d’un tri par sélection présenté dans le vidéogramme ou dans l’animation en ligne ci-dessus :
>> écrire l’algorithme de ce tri ;
>> programmer en langage Python une fonction qui implémente cet algorithme.
Principe du tri par fusion
- Algorithme : tri fusion
- Soit des entiers rangés dans un tableau T
- « Diviser » le tableau T en deux parties égales, à un élément près
- « régner » et « combiner » : les valeurs de chaque demi tableau sont comparées et placées par ordre croissant dans un tableau.
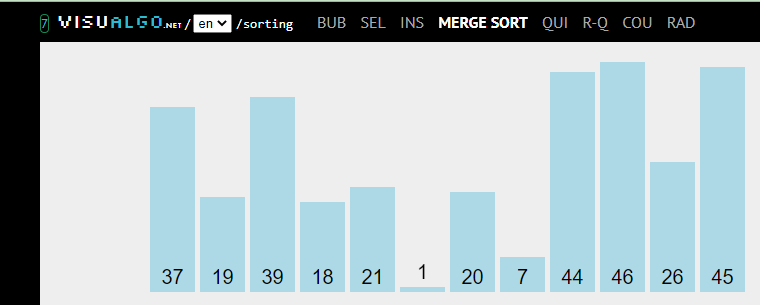
Exercice – Tri par fusion, version 1
En vous appuyant sur la principe du tri par fusion d’une part, et sur les commentaires fournis dans le code qui suit, compléter ce code afin d’implémenter une fonction qui réalise un tri par fusion (Remplacer les « @@@ » par ce qui convient).
"""Lycée - Terminale - Spécialité NSI | E-3 - Diviser pour régner."""
def triFusion(tableau):
"""Trier par fusion les valeurs de 'tableau'. Etape : 'diviser'.
Parameters
----------
tableau : LIST
Séquence de valeurs à trier.
Returns
-------
LIST
Séquence des valeurs triées par ordre croissant
"""
# condition de sortie des appels récursifs : le nombre d'éléments de
# 'tableau' est au plus égal à 1.
if len(tableau) @@@ :
return tableau
# 'milieu' : index de 'tableau' qui permet de diviser 'tableau' en deux
# parties égales, à 1 élément près.
# Calcul de la valeur de 'milieu'
milieu = @@@
# 'tableau_avant_milieu' : séquence des éléments de 'tableau' compris entre
# les index 0 et 'milieu'
tableau_avant_milieu = []
for i in range(@@@):
tableau_avant_milieu@@@
# 'tableau_apres_milieu' : séquence des éléments de 'tableau' compris entre
# l'index 'milieu' et l'index du dernier élément de 'tableau'
tableau_apres_milieu = []
for i in range(@@@):
tableau_apres_milieu@@@
return _triFusion(triFusion(tableau_avant_milieu),
triFusion(tableau_apres_milieu))
def _triFusion(t1, t2):
"""Trier par fusion. Etapes : 'résoudre et fusionner'.
Parameters
----------
t1 : LIST
Séquence de valeurs.
t2 : LIST
Séquence de valeurs.
Returns
-------
t : LIST
Séquences des valeurs de t1 et t2 triées par ordre croissant.
"""
t = [] # ce tableau va servir à stocker les valeurs triées
while t1 != [] and t2 != []:
if t1[0] <= t2[0]:
t.append(@@@)
del(@@@)
else:
t.append(@@@)
del(@@@)
# s'il reste des éléments dans la liste t1, on les ajoute à la fin de t.
if t1 != []:
@@@
# s'il reste des éléments dans la liste t2, on les ajoute à la fin de t.
if t2 != []:
@@@
return t
# Jeu de tests
if __name__ == "__main__":
t = [22, 3, 9, 19, 21, 5, 18, 1, 24, 4]
assert triFusion(t) == [1, 3, 4, 5, 9, 18, 19, 21, 22, 24]
t = [19, 4, 22, 24, 9, 1, 21, 3, 18, 5]
assert triFusion(t) == [1, 3, 4, 5, 9, 18, 19, 21, 22, 24]
t = [24, 22, 21, 19, 18, 9, 5, 4, 3, 1]
assert triFusion(t) == [1, 3, 4, 5, 9, 18, 19, 21, 22, 24]
Téléchargement du code complété
Nom du fichier : tri_fusion_1.py
Type du fichier : text/x-python
Taille du fichier : 3 Ko
Exercice – Tri par fusion, version 2
En vous appuyant sur la principe du tri par fusion d’une part, et sur les commentaires fournis dans le code qui suit, compléter ce code afin d’implémenter une fonction qui réalise un tri par fusion (Remplacer les « @@@ » par ce qui convient).
"""Lycée - Terminale - Spécialité NSI | E-3 - Diviser pour régner."""
def triFusion(tableau):
"""Trier par fusion les valeurs de 'tableau'.
Parameters
----------
tableau : LIST
Séquence de valeurs à trier.
Returns
-------
LIST
Séquence des valeurs triées par ordre croissant
"""
if len(tableau) > 1:
# Etape : 'Diviser'
# 'milieu' : index de 'tableau' qui permet de diviser 'tableau' en deux
# parties égales, à 1 élément près.
# Calcul de la valeur de 'milieu'
milieu = @@@
# 'tableau_avant_milieu' : séquence des éléments de 'tableau' compris
# entre les index 0 et 'milieu'
tableau_avant_milieu = []
for i in range(@@@):
tableau_avant_milieu@@@
# 'tableau_apres_milieu' : séquence des éléments de 'tableau' compris
# entre l'index 'milieu' et l'index du dernier élément de 'tableau'
tableau_apres_milieu = []
for i in range(@@@)):
tableau_apres_milieu@@@
triFusion(tableau_avant_milieu)
triFusion(tableau_apres_milieu)
# Etape : 'Régner' >>> résoudre et fusionner
i = 0 # index d'un élément de 'tableau_avant_milieu'
j = 0 # index d'un élément de 'tableau_apres_milieu'
k = 0 # index d'un élément de 'tableau'
while i < len(tableau_avant_milieu) and j < len(tableau_apres_milieu):
if tableau_avant_milieu[i] < tableau_apres_milieu[j]:
tableau[k] = tableau_avant_milieu[@@@]
i @@@
else:
tableau[k] = tableau_apres_milieu[@@@]
j @@@
k @@@
# s'il reste des éléments dans 'tableau_avant_milieu'
while i < len(tableau_avant_milieu):
tableau[k] = tableau_avant_milieu[@@@]
i @@@
k @@@
# s'il reste des éléments dans 'tableau_apres_milieu'
while j < len(tableau_apres_milieu):
tableau[k] = tableau_apres_milieu[@@@]
j @@@
k @@@
return t
# Jeu de tests
if __name__ == "__main__":
t = [22, 3, 9, 19, 21, 5, 18, 1, 24, 4]
assert triFusion(t) == [1, 3, 4, 5, 9, 18, 19, 21, 22, 24]
t = [19, 4, 22, 24, 9, 1, 21, 3, 18, 5]
assert triFusion(t) == [1, 3, 4, 5, 9, 18, 19, 21, 22, 24]
t = [24, 22, 21, 19, 18, 9, 5, 4, 3, 1]
assert triFusion(t) == [1, 3, 4, 5, 9, 18, 19, 21, 22, 24]
Téléchargement du code complété
Nom du fichier : tri_fusion_2.py
Type du fichier : text/x-python
Taille du fichier : 3 Ko
Terminaison de l’algorithme
Pour justifier la terminaison de l’algorithme, nous prouvons que le nombre d’appels récursifs est fini.
En effet les appels récursifs se font sur des tableaux dont la taille diminue de moitié (à un près) à chaque fois. Si n est la taille du tableau de départ, les valeurs successives de n seront : n/2, n/4, n/8, etc.
À l’issue de k appels récursifs la taille du tableau est de 1, ce qui interrompt les appels récursifs.
Correction de l’algorithme
Après k appels récursifs la taille du tableau est de 1, il s’agit donc d’un tableau trié.
Lors de la première fusion, la taille du tableau double (à 1 près) : le tableau fusionné est construit à partir des éléments de deux tableaux triés. C’est donc donc lui même un tableau trié.
Et donc en remontant de cette façon, lors de la dernière fusion, le tableau final possède la même taille que le tableau initial et comme il est construit à partir des éléments de deux tableaux triés, il sera lui même trié.
Coût de l’algorithme et comparaison avec d’autres algorithmes de tri-fusion
Le coût est d’abord lié au nombre k divisions de N par 2 qu’il faut réaliser pour obtenir deux tableaux ayant chacun 1 seul élément que l’on va comparer et fusionner, à partir d’un tableau initial ayant N éléments.
Or la valeur de k est telle que : 2k-1 < N ≤ 2k, ce qui est équivalent à k = log2 (N) arrondi à l’entier supérieur. Ou encore, pour toute valeur de N > 2, k correspond au nombre de chiffres – 0 ou 1 – qu’il faut pour écrire la valeur de N en binaire (Par exemple (12)10 = (1100)2, soit 4 chiffres, donc si N vaut 12 il faut 4 divisions).
Le coût est ensuite lié au nombre de comparaisons et d’affectations qu’il faut réaliser pour obtenir un tableau fusionné et trié.
Soit N1 et N2 les tailles respectives des deux tableaux à fusionner, il y aura au pire (N1+N2)-1 comparaisons et dans tous les cas N1+N2 affectations de valeurs pour former le tableau fusionné. Pour déterminer le coût on retient la plus grande de ces deux valeurs c’est à dire N1+N2. Et c’est lors de la dernière fusion que cette somme prendra sa plus grande valeur, à savoir N.
Donc le coût de cet algorithme peut s’exprimer de la façon suivante : k × N, ou d’une manière plus mathématiques : N × log2 (N). Le coût est donc « presque » linéaire.
| N = nombre de valeurs à trier | Tri-fusion | Tri par insertion ou par sélection |
| Coût | N × log2 (N) | N2 dans le pire des cas |
Cette méthode de tri est donc intéressante dès lors où le nombre de valeurs à trier est très grand.
Par exemple quand on double le nombre de valeurs à trier, le temps nécessaire pour trier va légèrement plus que doubler dans le cas du tri-fusion, alors qu’il peut être multiplié jusqu’à 4 fois dans le cas des deux méthodes de tri.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Rotation d’une image d’un quart de tour
Présentation du problème à résoudre

dimensions 256 pixels × 256 pixels


On cherche à écrire une fonction qui effectue la rotation à 90° d’une image « bitmap » en utilisant la méthode « diviser pour régner ».
Recherches préliminaires
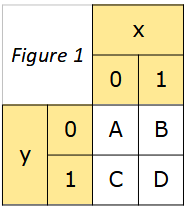
Considérons la matrice ci-contre (figure 1).
On implémente cette matrice en Python sous la forme d’un tableau de tableaux :
mat = [ [‘A’ , ‘B’] , [‘C’ , ‘D’] ]
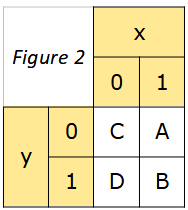
Écrire les instructions qui permettent de modifier cette matrice de la façon ci-contre (figure 2).
Corrigé (solution possible)
Nom du fichier : rotation_secteur.py
Type du fichier : text/x-python
Taille du fichier : 291 o
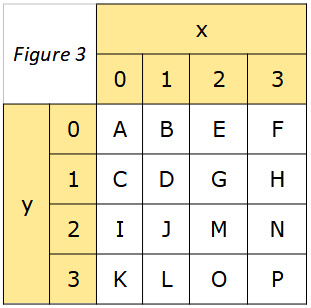
Considérons la matrice ci-contre (figure 3).
Écrire une implémentation de cette matrice en Python sous la forme d’une liste de listes.
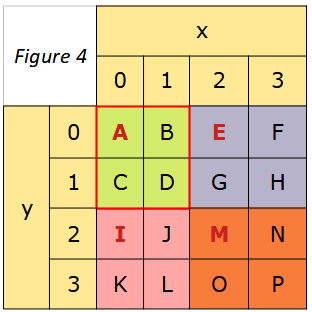
Écrire une fonction en Python appelée « rotation_secteur(mat, x, y, t) » dont les arguments sont une matrice, les coordonnées x et y de l’un des éléments de la matrice (voir figure 4) écrit en caractères gras et rouges d’une part et la taille t du secteur de cette matrice (la taille correspond au nombre de lignes ou de colonnes) d’autre part, qui permet de produire une rotation des éléments de l’un des quatre secteurs (figurés en fond colorés) de cette matrice, rotation de même nature que celle obtenue dans l’activité précédente.
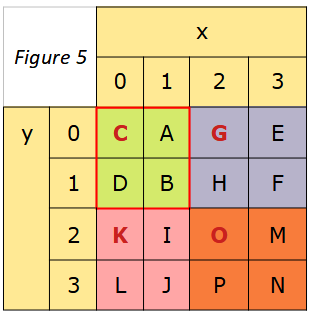
Puis écrire les appels à cette fonction qui permettent d’obtenir la rotation des éléments des quatre secteurs (voir figure 5).
Corrigé (solution possible)
Nom du fichier : rotation_secteur-1.py
Type du fichier : text/x-python
Taille du fichier : 2 Ko
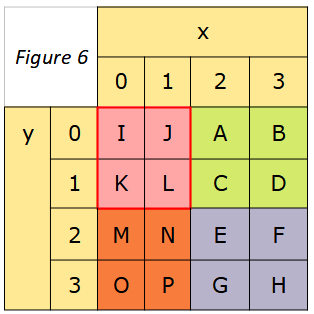
Écrire une fonction en Python appelée « rotation_matrice(mat, x, y, t) » dont les arguments sont ‘mat’ une matrice (figure 4), les coordonnées x et y de l’un des éléments de cette matrice, la taille t de cette matrice, et qui permet de produire une rotation des quatre secteurs (figurés en fond colorés) de la matrice (figure 6).
Corrigé (solution possible)
Nom du fichier : rotation_matrice.py
Type du fichier : text/x-python
Taille du fichier : 529 o
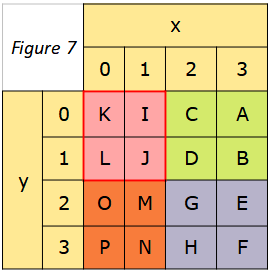
En s’inspirant des fonctions écrites dans les activités précédentes, écrire une fonction unique en Python appelée « rotation_90_matrice(mat, x, y, t) » dont les arguments sont ‘mat’ une matrice comme celle de la figure 4, les coordonnées x et y de l’un des éléments de cette matrice, la taille t de cette matrice, et qui permet de produire une rotation à 90° de la matrice (pour obtenir celle de la figure 7)
Corrigé (solution possible)
Nom du fichier : rotation_matrice-90
Type du fichier : text/x-python
Taille du fichier : 807 o
Corrigé (solution possible) -Version récursive
Nom du fichier : rotation_matrice-90-rec.py
Type du fichier : text/x-python
Taille du fichier : 949 o
Mise en application avec une « véritable » image
- Copier et coller le code qui suit dans un éditeur/interpréteur Python (ex : Pyzo, Spyder).
- Sauvegardez ce code dans un dossier.
"""Lycée - Terminale - Spécialité NSI | E-3 "Diviser pour régner."""
from PIL import Image
# le fichier 'image.png' doit se trouver dans le même dossier que ce fichier Python
img = Image.open("image.png")
# assignation de la largeur et de la hauteur, en pixels, de l'image chargée
largeur,hauteur = img.size
print(largeur)
print(hauteur)
# création d'une matrice des pixels de l'image
matrice = img.load()
# 0 ≤ x < largeur | 0 ≤ y < hauteur
# matrice[x,y] renvoie un tuple (rouge, vert, bleu, transparence)
# 0 ≤ rouge ≤ 255
# 0 ≤ vert ≤ 255
# 0 ≤ bleu ≤ 255
# 0 ≤ transparence ≤ 255
print(matrice[120,120])- Téléchargez le fichier « image.png » et placez le dans le même dossier que le code d’avant.
https://sapiensjmh.top/filerun/wl/?id=Qm9EMkHy62vexf0LgKyiDSdhPzrsrtOb - Testez le code : lancez son exécution et vérifiez qu’aucun message d’erreur ne s’affiche.
L’image chargée ici est carrée et ses dimensions correspondent à une puissance de 2 (256 = 28).
L’idée est de diviser cette image en quatre parties de façon récursive, jusqu’à obtenir 4 images d’un seul pixel. On effectue alors une rotation de ces quatre pixels :
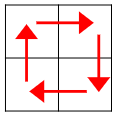
En s’inspirant de la fonction ‘rotation_90_matrice’, et des indications fournies au début de cet exercice, écrire en Python une fonction ‘rotation_bmp(matrice, x, y, px)’ qui effectue la rotation d’une image ‘bipmap’ dont les pixels sont chargés dans une matrice, et dont le nombre de pixels en largeur et hauteur vaut ‘px’, x et y étant les coordonnées du pixel situé en haut à gauche de la matrice.
Tester le ‘bon’ fonctionnement de cette fonction. Pour cela, ajouter l’instruction ‘img.save(« rotation.png »)’ après l’appel de la fonction ‘rotation_bmp(matrice, x, y, px)’, puis vérifier dans le dossier où se trouvent les fichiers Python et ‘ image.png ‘ la présence d’un nouveau fichier ‘rotation.png’ contenant l’image ayant effectué une rotation de 90°.
Corrigé (solution possible) – Version avec choix du sens de rotation
Nom du fichier : rotation_image_90_v2.py
Type du fichier : text/x-python
Taille du fichier : 1 476 octets